¿Qué son las Matemáticas?
Tipos de aplicaciones
En matemáticas los conjuntos se pueden representar usando diagramas de Venn.
Dado el conjunto $X=\{a, b, c\},$ lo podemos representar por:
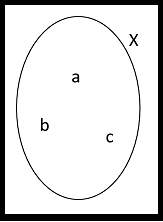 | |
Cuando queremos representar una función entre dos conjuntos usando diagramas de Venn,
representamos ambos conjuntos y pintamos flechas que definen la aplicación. Por ejemplo,
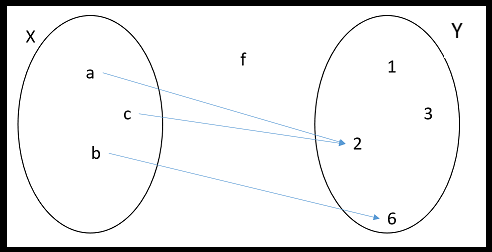
si tomamos $X=\{a, b, c\}$ e $\,Y=\{1,2,3,6\}$, podemos definir la aplicación $F=\{(a,2),(b,6),(c,2)\}$.
En la forma usual, esta aplicación se escribe como $f:X\longrightarrow Y$, definida por
$f(a)=2$, $f(b)=6$ y $f(c)=2$.
Usando diagramas de Venn se representa por:
| |
| | | |
| |  | |
$\bigstar$ Sean $X$ e $Y$ dos conjuntos no vacíos.
Se dice que $\,f:X\longrightarrow Y$ es sobreyectiva si para todo $y \in Y$ existe $x\in X$ tal que $f(x)=y$.
Si la aplicación $f$ esta representada como subconjunto del producto cartesiano $X\times Y$,
tenemos que $F$ es sobreyectiva si cualquier elemento de $Y$ aparece como segunda coordenada de algún
elemento de $F$. En el ejemplo anterior, vemos que $F=\{(a,2),(b,6),(c,2)\}$ no es sobreyectiva,
ya que hay dos elementos ($1$ y $3$) que no aparecen como segunda coordenada en ninguno de los elementos de $F$.
Si la aplicación $f$ se representa por medio de diagramas de Venn, entonces $f$ es
sobreyectiva si a cada elemento de $Y$ le llegua alguna flecha (puede ser una o más de una).
En el ejemplo anterior, a los elementos $1$ y $3$ no le llega ninguna flecha, por lo que $f$ no es sobreyectiva.
Veamos otros ejemplos:
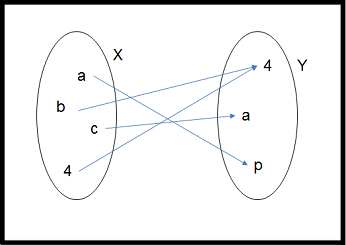 | 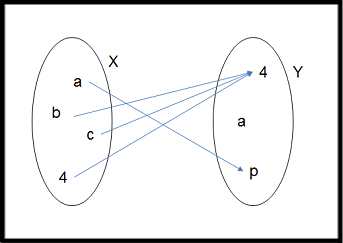 |
| $F:=\{(a,p),(b,4),(c,a),(4,4)\}$ | $G:=\{(a,p),(b,4),(c,4),(4,4)\}$ |
| Sobreyectiva | No sobreyectiva |
En general, no es fácil saber si una aplicación es o no sobreyectiva.
Por ejemplo, $f:\mathbb{R}\to \mathbb{R}$ definida por $f(x)=x^2$ ¿es sobreyectiva?
$\bigstar$ Sean $X$ e $Y$ dos conjuntos no vacíos.
Se dice que $\,f:X \longrightarrow Y$ es inyectiva si para todo par de elementos $x_1,x_2\in X$, siendo $x_1\ne x_2$, se tiene que $f(x_1)\ne f(x_2)$.
Expresado de una manera más informal, una aplicación es inyectiva si siempre que se tengan dos elementos distintos de $X$,
estos "van a parar" a elementos distintos de $Y$. Si la aplicación $f$ está representada como subconjunto del producto
cartesiano $X\times Y$, tenemos que $F$ es inyectiva si no se repite ninguna segunda coordenada de los elementos de $F$.
En términos de diagramas de Venn, para comprobar si una aplicación es inyectiva tenemos que ver
que a ningún elemento de $Y$ le llegan dos flechas (a cada uno le puede llegar una flecha o ninguna).
Veamos otros ejemplos:
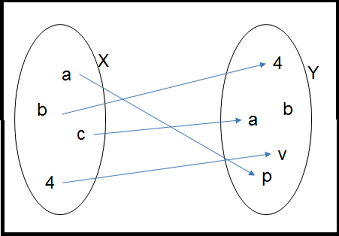 | 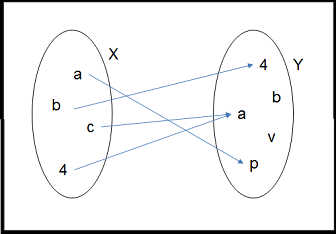 |
| $F:=\{(a,p),(b,4),(c,a),(4,v)\}$ | $G:=\{(a,p),(b,4),(c,a),(4,a)\}$ |
| Inyectiva | No inyectiva |
Como ejercicio, dada $f:\mathbb{R}\to \mathbb{R}$ definida por $f(x)=x^2$ ¿es inyectiva?
$\bigstar$ Sean $X$ e $Y$ dos conjuntos no vacíos.
Se dice que $\,f:X \longrightarrow Y$ es biyectiva si es al mismo tiempo inyectiva y
sobreyectiva. Esto quiere decir que para todo elemento $y \in Y$ existe un único elemento $x\in X$ tal que $f(x)=y$ (existe, por ser sobreyectiva, y es único,
por ser inyectiva).
Si la aplicación $f$ está representada como subconjunto del producto
cartesiano $X\times Y$, entonces $F$ es biyectiva
si cualquier elemento de $Y$ aparece como segunda coordenada de un
elemento de $F$ (sólo una vez).
En términos de diagramas de Venn, una aplicación es biyectiva si a cada elemento de $Y$ le llega una flecha y sólo una.
También se cumple que de cada elemento de $X$ sale una
flecha y sólo una (esto es cierto para cualquier aplicación).
Podemos pensar entonces que en una aplicación biyectiva cada elemento del conjunto $X$
está "emparejado" con un elemento del conjunto $Y$, de manera que una vez que se
han formado estas "parejas", no falta ni sobra nigún elemento ni en un
lado ni en el otro.
Como ejercicio, poner un ejemplo de aplicación biyectiva por medio de
diagramas de Venn.
En los ejemplos que hemos visto anteriormente (diagramas de Venn), la aplicación no es biyectiva. ¿Se
puede modificar en alguno de ellos la aplicación para
que sea biyectiva, dejando los mismos conjuntos $X$ e $Y$?
¿Qué se observa sobre el número de elementos
de los conjuntos?
Dada $f:\mathbb{R}\to \mathbb{R}$ definida por $f(x)=x^3$ ¿es biyectiva?





